📝 The Tunnel of Samos- Tom Apostol

Samos, Greece: 6th Century BC.

In the era of building civilisations and a time of no formal mathematical inscriptions, Eupalinos of Samos, an architect at the time built the Tunnel of Samos, modern day Greece. The Tunnel of Samos is one of the first known geometry-based approach to successfully building a two-opening aqueduct through a mountain. Considering that the father of Mathematics, Pythagoras was also born here years after this accomplishment, it could be safe to say that the Greeks in Samos held great intellect and common sense.

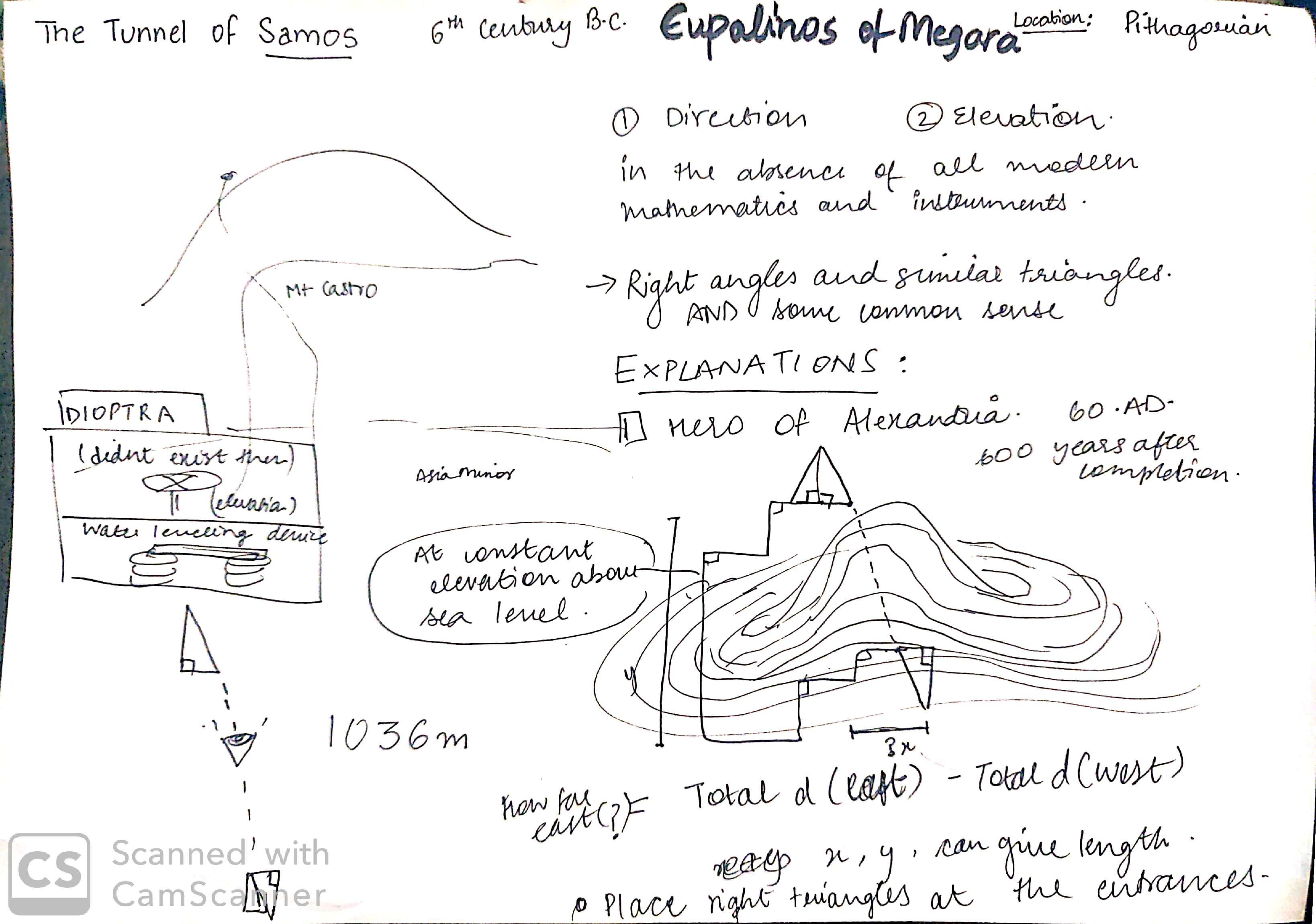
To understand: Imagine a mountain with a tunnel passing through. In order to be built, it would need builders from either end meeting in the center, completing the tunnel. How could they have known, on either ends where to start and which direction to move towards?

In order to be successful, they would need to a) Be at the same elevation above sea level and, b) be moving towards each other (direction). So how did Eupalinos of Samos solve this problem?

[Hint: It was a certain 3 sided polygon. And a little bit of common sense.] And it is genius.

Thought: I wonder if our modern day complex solutions could now be ‘optimised’ with the same old previously incompetent solutions. Befriending the artificial intelligence, obviously.

Source: The Tunnel of Samos- Tom Apostol